Incertidumbre de medición: Nueva definición e impacto

Deja un comentario / Sin categoría / Por

Introducción

La incertidumbre de medición es uno de esos términos que usamos todos los días en metrología y acreditación, es una piedra angular, pero también puede ser fuente de confusión: ¿Es un número, una idea o ambas cosas?

Recientemente, el Joint Committee for Guides in Metrology (JCGM) del Bureau International des Poids et Mesures (BIPM) propuso cambiar la definición de incertidumbre de medición para demarcar la separación entre concepto y expresiones cuantitativas (incertidumbre estándar, intervalos de cobertura, matrices de covarianza), ampliando la aplicabilidad a mediciones multivariadas, conteos discretos y resultados obtenidos del uso de IA (Inteligencia Artificial) sin alterar la práctica diaria del laboratorio.

JCGM Webinar: Have Your Say on the Future Definition of ‘Measurement Uncertainty’

Esto ha generado preguntas legítimas en técnicos, auditores y responsables de calidad: ¿Cambia la forma en que calculo la incertidumbre de medición? ¿Debo rehacer procedimientos o certificados? ¿Qué implica para la acreditación ISO/IEC 17025 y la enseñanza en metrología

En este artículo veremos, con ejemplos ¿Por qué una definición flexible es necesaria? ¿Qué cambia (y qué no)? ¿Qué implicaría para la redacción de certificados? Y algunas sugerencias de ¿Cómo aplicar este enfoque en el trabajo cotidiano en un laboratorio de calibración que sigue los lineamientos del estándar ISO/IEC 17025?

Tabla de contenido
  1. Introducción
  2. ¿Qué propone el JCGM?
  3. ¿Por qué importa? — motivos técnicos y pedagógicos
  4. Implicaciones terminológicas y el VIM (WG1 vs WG2)
  5. Definición actual vs. nueva propuesta (comparativa)
  6. ¿Cambia algo en la práctica?
  7. Herramientas y representaciones de la incertidumbre
  8. Ejemplo: Conteo de latas (inspirado en el Webinar)
  9. Conclusiones
  10. Próximos pasos (SUGERENCIAS):
  11. Recursos y referencias

¿Qué propone el JCGM?

La propuesta del JCGM para la próxima edición del VIM (VIM4) sugiere que la definición de la incertidumbre pase de enunciado cuantitativo a un enunciado conceptual:

«Doubt about the value of the measurand that remains after making a measurement.»
VIM 4

Cuya traducción al español sería:

«Duda sobre el valor del mensurando (la medida) que permanece después de realizar una medición.«
VIM 4

En el Webinar del JCGM se enfatiza que la incertidumbre es un estado de conocimiento (subjetivo pero racional) y no necesariamente un único parámetro numérico. Dicha definición está acompañada de notas que indican que esa duda puede describirse por distribuciones de probabilidad, intervalos de cobertura, incertidumbres estándar, matrices de covarianza o regiones de cobertura.

¿Por qué importa? — motivos técnicos y pedagógicos

La razón central del JCGM para proponer una nueva definición es que llamar a la incertidumbre un “parámetro” limitaba conceptual y operativamente la forma de representarla.

Redefinirla como duda amplía su aplicabilidad, sin invalidar los enfoques cuantitativos ya conocidos. Esto es especialmente útil cuando la representación natural de la duda es una distribución, una matriz de covarianza o incluso una probabilidad discreta.

Desde el punto de vista técnico, la metrología moderna enfrenta:

  • Mediciones multivariadas: cuando trabajas con vectores de resultados (p. ej., calibración de un conjunto de pesas), un solo número no describe las dependencias entre variables, obliga a pensar en matrices de covarianza al combinar elementos correlacionados
  • Datos discretos y clasificación: conteos exactos o respuesta entregadas por IA (Inteligencia Artificial) requieren representaciones distintas (distribuciones discretas, probabilidades de clasificación).
  • Métodos modernos: Monte Carlo e inferencia bayesiana encajan mejor si la incertidumbre se trata como “estado del conocimiento”.

Desde el punto de vista pedagógico, nos otorga:

  • Claridad conceptual: Evita la ambigüedad entre concepto y medida cuantitativa (por ejemplo, confundir “incertidumbre” con “incertidumbre estándar”).
  • Mejor comunicación: Permite explicar a clientes y auditores que la incertidumbre representa el grado de confianza en un resultado, y que esa confianza puede expresarse por varios medios.

Implicaciones terminológicas y el VIM (WG1 vs WG2)

  • WG1 (GUM): propone la definición subjetiva (duda) para eliminar ambigüedades entre concepto y sus expresiones.
  • WG2 (VIM): muestra cautela por las reglas de terminología (ISO 704/1087) y por la necesidad de preservar entradas cuantitativas en el vocabulario.

Resultado práctico: la solución propuesta por WG2 es reordenar definiciones derivadas para que las entradas cuantitativas (por ejemplo: “incertidumbre de medición estándar”) comiencen por el término cuantitativo (“desviación estándar que expresa la incertidumbre…”), garantizando coherencia terminológica y preservando su carácter cuantitativo.

Definición actual vs. nueva propuesta (comparativa)

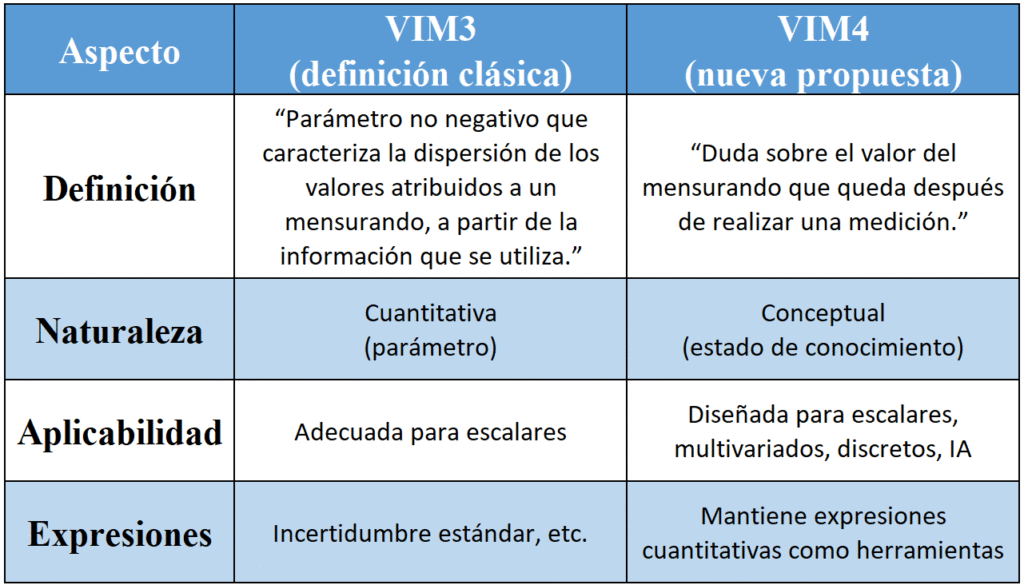
Conclusión: la nueva definición aporta flexibilidad conceptual sin invalidar las herramientas numéricas que ya usas.

¿Cambia algo en la práctica?

Respuesta rápida: NO CAMBIA los cálculos ni los requisitos de acreditación (tus métodos, fórmulas y reportes siguen igual); MEJORA CÓMO LO COMUNICAS.

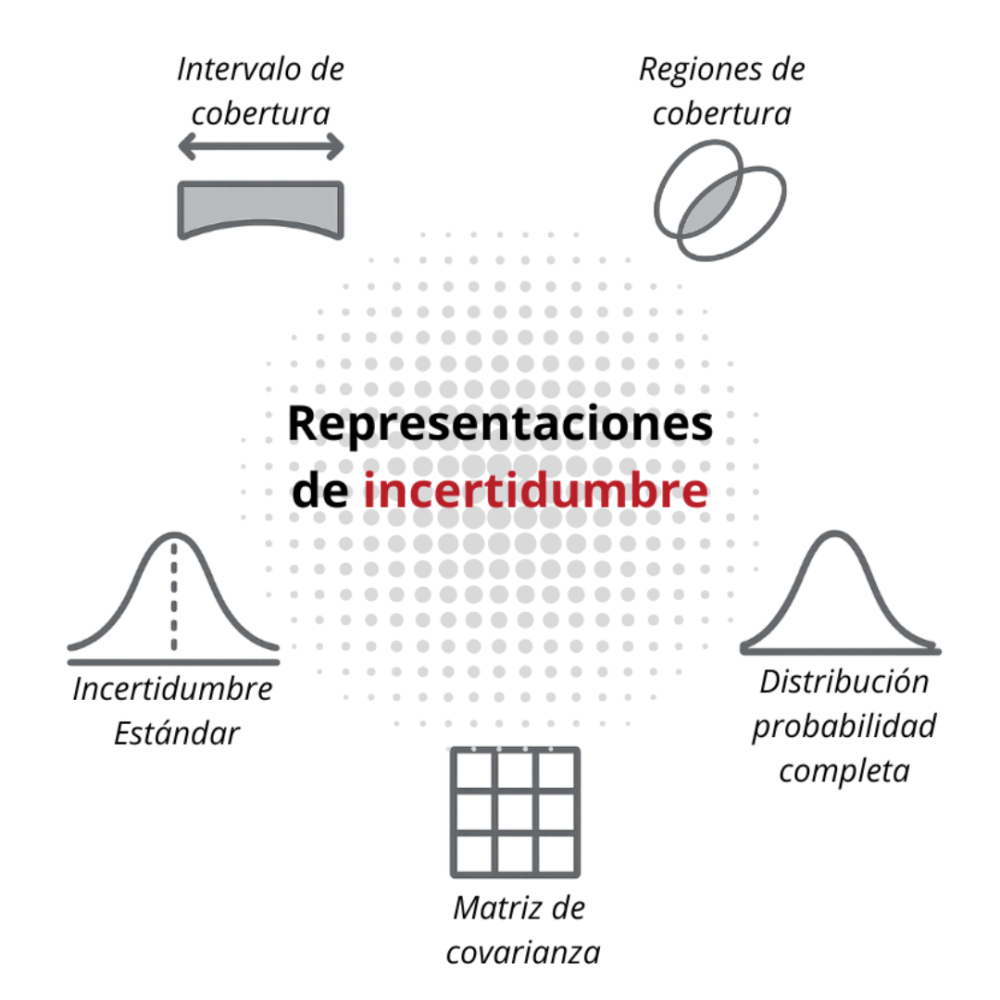
Herramientas y representaciones de la incertidumbre

La propuesta abre la puerta a representar la duda con la herramienta adecuada según el problema:

  1. Incertidumbre estándar — cuando la distribución es bien aprox. por una desviación estándar.
  2. Intervalo de cobertura / incertidumbre expandida — útil para comunicar rangos con probabilidad asociada.
  3. Distribución de probabilidad completa — la descripción más completa del estado del conocimiento (continua o discreta).
  4. Matriz de covarianza — esencial en mediciones multivariadas (representa correlaciones entre componentes).
  5. Regiones de cobertura — extensión multivariada de intervalos unidimensionales.

Consejo práctico: Documenta qué representación estás usando y por qué, en el certificado o informe. Esto evita malos entendidos con clientes no técnicos.

Ejemplo: Conteo de latas (inspirado en el Webinar)

Situación: recibes una caja con 12 latas. Las cuentas y obtienes el valor 12.

  • En este caso, el mensurando es un valor entero y, si el conteo fue correcto, la “duda” es esencialmente nula, no existe incertidumbre intrínseca (salvo error humano o de muestreo). La nueva definición permite expresar la incertidumbre de forma discreta (probabilidad concentrada en 12) en lugar de forzar una desviación estándar arbitraria.

PERO: si la incertidumbre es la duda restante tras el conteo y contemplamos una posibilidad de error de conteo ±1 debido a un error humano. Se podría describir con una distribución discreta.

  • Imaginemos (no cuesta nada) que realizamos un experimento dónde podemos contar la cantidad de latas 10 veces, por ejemplo, y de dicha EXPERIENCIA podemos observar que debido a un «error humano«, en el conteo, hay un 10% de probabilidad (1 vez en 10 conteos de las 12 latas) de equivocarse al contar de menos, un 10% de equivocarse al contar de más, y un 80% de que el conteo sea exacto.
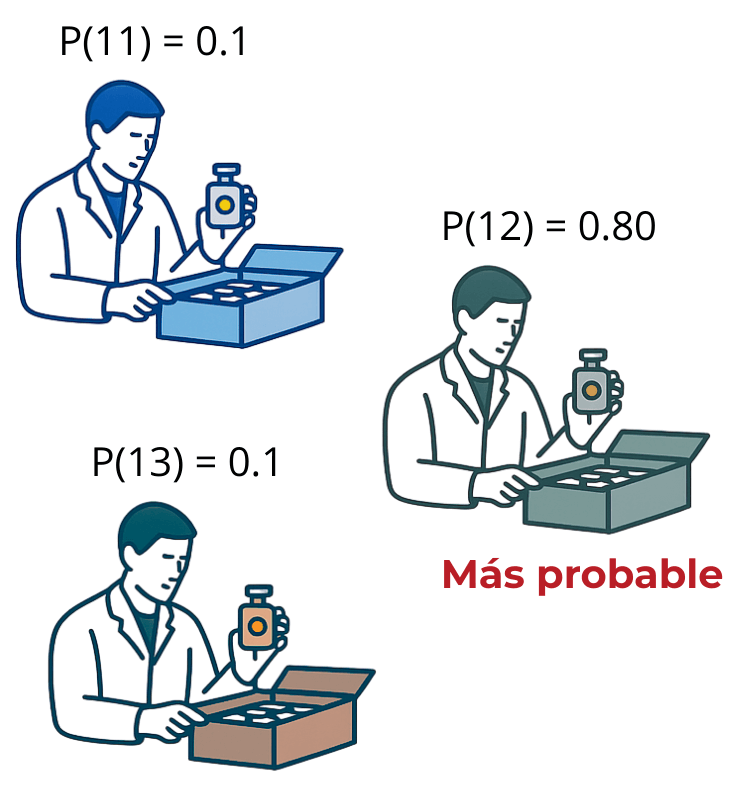
  • Esto daría una distribución como: (P(12) = 0.80, P(11) = 0.1, P(13) = 0.1). Esto no es otra cosa que, una forma de modelar el conocimiento o supuestos sobre la veracidad de una observación.

¿Por qué este ejemplo es importante? Porque ilustra que no todas las mediciones son continuas y que la representación de la incertidumbre debe ajustarse a la naturaleza del mensurando. Así, evitamos aplicar herramientas continuas cuando la estructura del dato es discreta.

Conclusiones

La propuesta del JCGM de redefinir la incertidumbre de medición como «duda sobre el valor del mensurando…» aporta una claridad conceptual valiosa y amplía la aplicabilidad de la metrología a problemas modernos (IA, multivariados, datos discretos), sin cambiar la práctica de laboratorio ni los cálculos que aplicas a diario. Lo relevante para tu trabajo, a nivel técnico es: entender qué representación usar para tus resultados y documentar claramente cómo expresas esa duda en informes y certificados.

DATO CURIOSO: el National Institute of Standards and Technology (NIST) ya adoptó este enfoque desde hace un buen tiempo, lo que refuerza la validez operativa de la propuesta…

Próximos pasos (SUGERENCIAS):

Aunque esto haya sido presentado como una propuesta podría “tocar nuestra puerta” en cualquier momento, con ello en mente, te propongo algunos pasos que podrían allanar el camino, en otras palabras, Posibles riesgos y cómo evitarlos:

❌ Olvidar actualizar documentos internos:

✅ Revisa los procedimientos y formatos de tu laboratorio y haz las actualizaciones necesarias, ya que, la coherencia terminológica es clave en auditorías ISO/IEC 17025.

✅ Añade notas que expliquen qué representa “incertidumbre de medición” (concepto) y qué expresión se ha usado (incertidumbre estándar, intervalo, matriz).

✅ Actualiza procedimientos internos, en especial el procedimiento de cálculo de incertidumbre, añade una sección sobre identificación del tipo de mensurando (escalar/multivariado/discreto).

❌ Olvidar capacitar a tu personal del laboratorio:

✅ Programa (al menos) una sesión teórico-práctica, interna o externa, sobre los cambios. Ya que, aunque el cambio es terminológico y no metodológico, una cosa es la definición y otra, muy diferente, su expresión numérica y/o algebraica (cálculo “clásico” GUM, matrices de covarianza, Monte Carlo)

✅ Asegúrate de que los instructores enfaticen la distinción entre concepto ↔ expresión en cursos sobre la GUM (JCGM 100) y/o ISO/IEC 17025.


¿Te interesan estos temas? Comparte este artículo con tus colegas y/o en tus redes sociales. Porque la calidad es una puerta abierta, para aquellos dispuestos a moverse.

La teoría cobra sentido cuando se aplica y aprender no debería ser un proceso confuso ni fragmentado. Con mi metodología transformo conceptos complejos en conocimiento claro, aplicable y estructurado, ese es el sello de XMET. Escríbeme a info@xmet.com.co si deseas llevar estos temas a la acción, en el laboratorio de calibración.

Recursos y referencias

Deja un comentario